Introduction to Neural Networks

Neural networks

Neural networks are a collection of artificial neurons connected together so it's best to start by learning about about neurons.

In nature, a neuron is a cell which has an electrical connection to other neurons. If a charge is felt from 'enough' of the input neurons then the neuron fires and passes a charge to its output. This design and how they are arranged into networks is the direct inspiration for artificial neural networks.

An artificial neuron has multiple inputs and can pass its output to multiple other neurons.

A neuron will calculate its value, $p = \sum_i{x_iw_i}$ where $x_i$ is the input value and $w_i$ is a weight assigned to that connection. This $p$ is then passed through some activation function, $\phi()$, to determine the output of the neuron. The activation function's job is to introduce some non-linearity between layer, allowing you to solve more complex problems.

The final equation for a node is therefore:

$$o = \phi(\sum_i{x_iw_i})$$

Networks

The inputs to each neurons either come from the outputs of other neurons or are explicit inputs from the user. This allows you to connect together a large network of neurons:

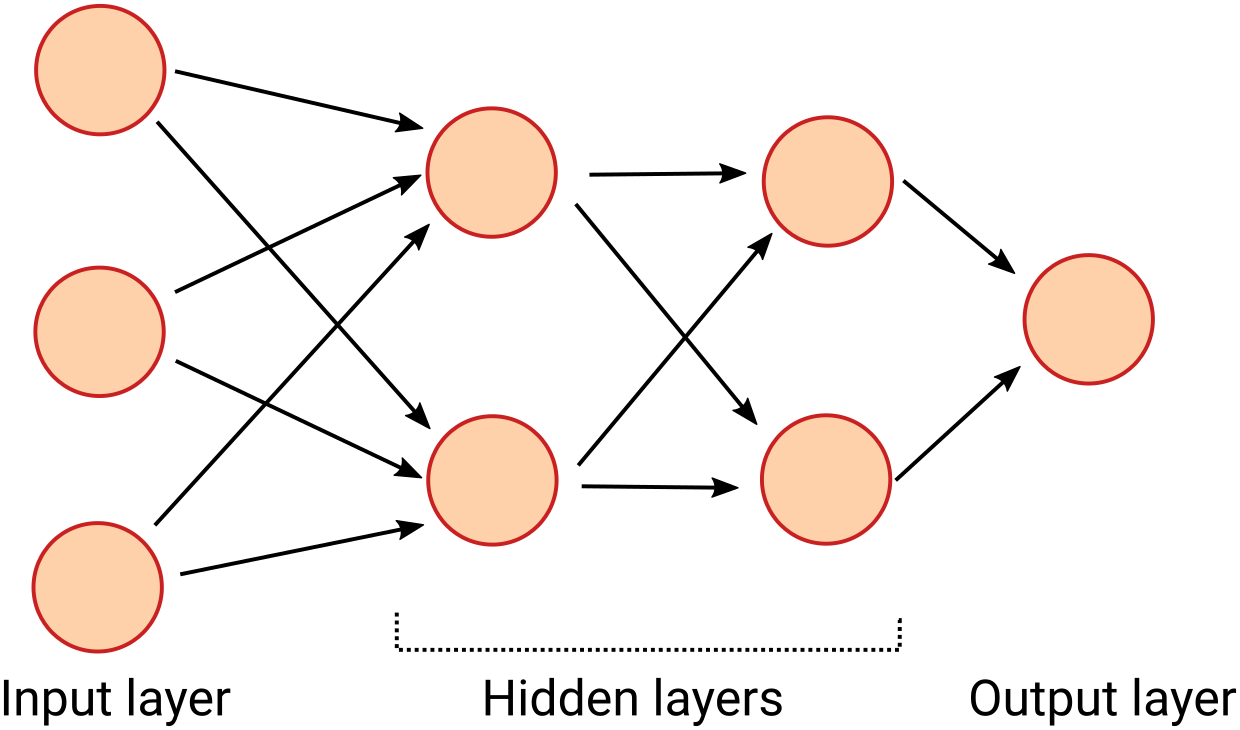
In this network every neuron on one layer is connected to every neuron on the next. Every arrow in the diagram has a weight assigned to it.

You input values on the left-hand side of the network, and the data flows through the network from layer to layer until the output layer has a value.

What shape should the network be?

There is some art and some science to deciding the shape of a network. There are rules of thumb (hidden layer size should be similar sized to the input and output layers) but this is one of the things that you need to experiment with and see how it affects performance.

The number of hidden layers relates to the level of abstraction you are looking at. Generally, more complex problems need more hidden layers (i.e. deeper networks) but this makes training harder.

How are the weights calculated?

The calculation of the weights in a network is done through a process called training. This generally uses lots of data examples to iteratively work out good values for the weights.

How do you train neural networks

The main method by which NNs are trained is a technique called backpropagation.

In order to train your network you need a few things:

• A labelled training data set
• A labelled test (or evaluation) data set
• A set of initial weights

Initial weights

The weights to start with are easy: just set them randomly!

Training and testing data sets

You will need two data sets. One will be used by the learning algorithm to train the network and the other will be used to report on the quality of the training at the end.

It is important that these data sets are disjoint to prevent overfitting.

It is common to start with one large set of data that you want to learn about and to split it into 80% training data set and 20% test data set.

Backpropagation ("the backward propagation of errors")

Once you have your network structure, your initial weights and your training data set, you can start training.

There have been lots of algorithms to do this over the last several decades but the currently most popular one is backpropagation.

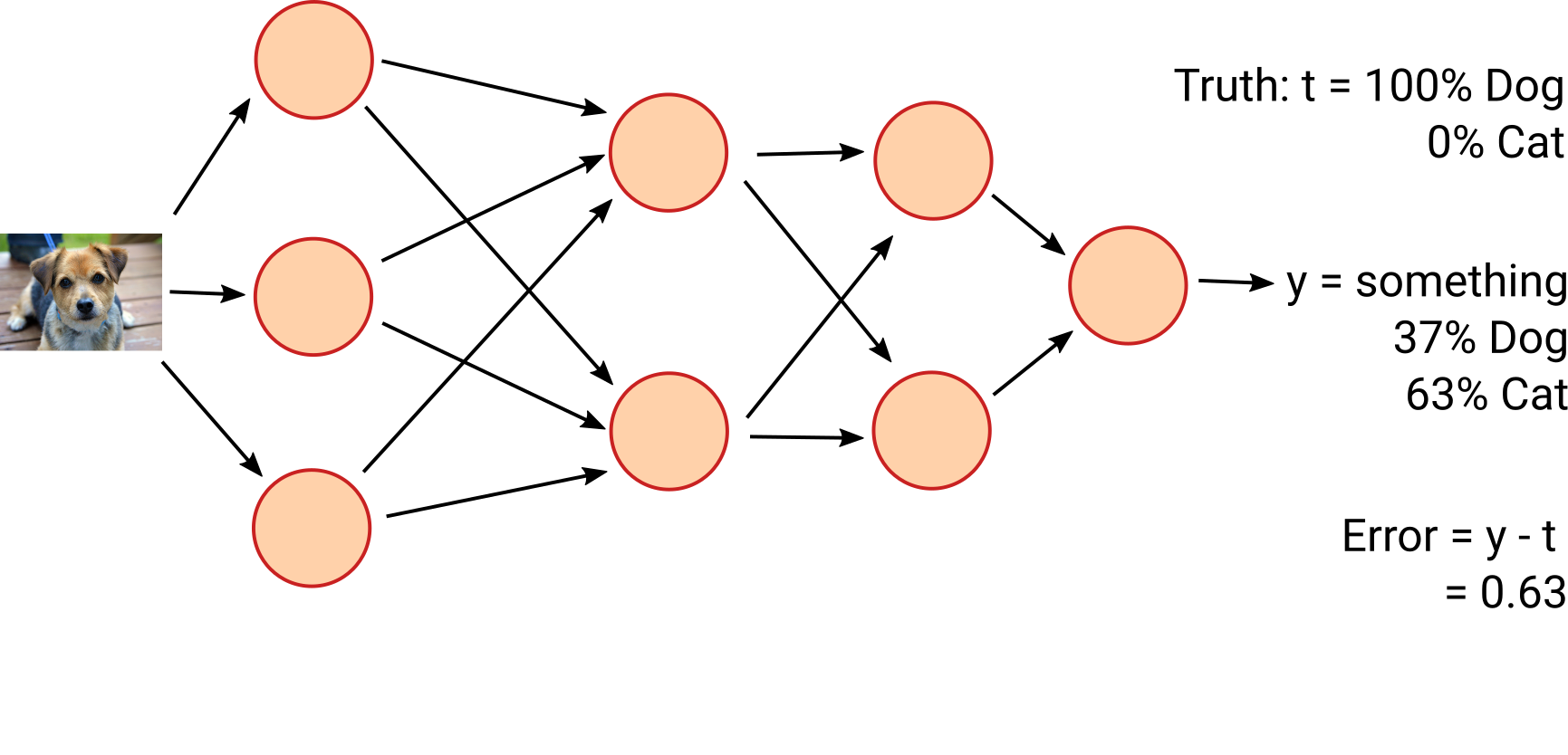
First, we define our loss function, a measure of "how wrong" we are. For example, $J(y) = (t-y)^2$ where $y$ is the output of the network and $t$ is what we want the output to be.

We then calculate its derivative with respect to each weight, $D_n(y) = \frac{dJ(y)}{dw_n}$. This gives how much you need to tweak each weight—and in which direction—to correct the output.

Then for each training entry:

1. pass it through the network and find the value $y$
2. tweak each weight by $\delta w_n = -R D_n(y)$ where $R$ is the learning rate

This means that the 'more wrong' the weights are, the more they move towards the true value. This slows down as, after lots of examples, the network converges.

Common neural network libraries

It would, as with with most things, be possible to to the above by hand but that would take years to make any progress. Instead we use software packages to do the leg work for us.

The can in general, construct networks, automatically calculate derivatives, perform backpropagation and evaluate performance for you.

Some of the most popular are:

• PyTorch
• TensorFlow
• scikit-learn

In this workshop, we will be using TensorFlow.

Previous | Next